实验一:数制转换
实验名称:实现十进制整数 N 向其它进制数 d(二、八、十六)的转换。
【数据结构】
#define S_SIZE 100 //栈的空间大小
#define STACKINCREAMENT 10 //增加空间
struct SqStack{
int *base; //栈底
int *top; //栈顶
int stacksize; //栈当前的存储空间
};
【算法思想】
void InitStack(SqStack &S); //初始化空栈
int StackEmpty(SqStack S); //判空
void GetTop(SqStack S, int &e);//获得栈顶元素
void push(SqStack &S, int e);//进栈
void pop(SqStack &S, int &e);//出栈
void convert(SqStack &S, int N, int n);//十进制转 N 进制
unsigned n, N;//要转换成的进制数和要转换的数
SqStack s;
InitStack(s);//初始化空栈
printf("输入要转换的十进制数和要转换为的进制数:\n");
scanf("%d,%d", &N, &n);
printf("%d 转换为%d 进制后为:\n", N, n);
convert(s, N, n);
【算法描述】
void InitStack(SqStack &S)
{
S.base = (int *)malloc(S_SIZE*sizeof(int));
S.stacksize = S_SIZE;
S.top = S.base;//初始化空栈
}
int StackEmpty(SqStack S)
{
if (S.base == S.top)
return 1;
else
return 0;
}
void GetTop(SqStack S, int &e)
{//获得栈顶元素
e = *(S.top - 1);
}
void push(SqStack &S, int e)
{//进栈
if (S.top - S.base >= S.stacksize)
{
S.base=(int *)realloc(S.base,(S.stacksize+STACKINCREAMENT)*sizeof(int));
S.top=S.base+S.stacksize;
S.stacksize+=STACKINCREAMENT;
}
*(S.top)=e;
S.top++;
}
void pop(SqStack &S,int &e)
{//出栈
if(S.base !=S.top)
{
S.top--;
e=*S.top;
}
}
void convert(SqStack &S, int N,int n)
{
InitStack(S);
do{
push(S,N%n);
N /= n;
}while(N!=0);
int e;
while(!StackEmpty(S))
{
pop(S,e);
if(e>9)//十六进制时输出字母
{
e=e+55;
printf("%c",e);
}else
printf("%d",e);
}
printf("\n");
}

实验二:单链表的插入删除
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#define M 100
typedef int Etype; //定义单链表结点值的类型为整型
typedef struct Node
{
Etype data; //单链表中的数据域
struct Node *link; //单链表的指针域
}Node;
typedef Node *List; //定义单链表
List BuildList1();
List BuildList2();
void PrintList(List first);
void clear(List *first);
//头插法建立链表
List BuildList1()
{
Node *L;
Etype x,n;
L = (Node *)malloc(sizeof(Node)); //申请头结点空间
L->link = NULL; //初始化一个空链表printf("请输入元素个数:\n");
scanf("%d",&n);
printf("请输入元素:\n"); //x 为链表数据域中的数据
for(int i=0;i<n;i++)
{
scanf("%d",&x);
Node *p;
p = (Node *)malloc(sizeof(Node)); //申请新的结点
p->data = x; //结点数据域赋值
p->link = L->link; //将结点插入到表头 L-->|2|-->|1|-->NULL
L->link = p;
}
return L;
}
//尾插法建立链表
List BuildList2()
{
Node *L,*r;
Etype n,x;
L = (Node *)malloc(sizeof(Node)); //申请头结点空间
L->link = NULL; //初始化一个空链表
printf("请输入元素个数:\n");
scanf("%d",&n);
r = L; //r 始终指向终端结点,开始时指向头结点
printf("请输入元素:\n");
for(int i=0;i<n;i++)
{
scanf("%d",&x);
Node *p;
p = (Node *)malloc(sizeof(Node)); //申请新的结点
p->data = x; //结点数据域赋值
r->link = p; //将结点插入到表头 L-->|1|-->|2|-->NULL
r = p;
}
r->link = NULL;
return L;
}
//输出链表
void PrintList(List first)
{
Node *Li;
if(first==NULL)
{
printf("链表为空!\n");
return;
}
Li=first->link;
while(Li!=NULL)
{
printf("%d ",Li->data);
Li=Li->link;
}
printf("\n");
}
//清空链表
void clear(List *first)
{
Node *p=*first;
while(*first)
{
p=(*first)->link;
free(*first);
*first=p;
}
}
int main()
{
Node *L;
L=BuildList1(); //调用 BuiltdList1(前插法)建立单链表算法
PrintList(L); //打印单链表
clear(&L);//清空单链表
L=BuildList2(); //调用 BuiltdList2(后插法)建立单链表算法
PrintList(L); //打印单链表
clear(&L);//清空单链表
}
实验三:二叉树的遍历
#include<iostream.h>
struct BiNode
{
char data;
BiNode *lchild,*rchild;
};
class BiTree
{
public:
BiTree(){root=Creat(root);}
~BiTree(){Release(root);}
void PreOrder(){PreOrder(root);}
void InOrder(){InOrder(root);}
void PostOrder(){PostOrder(root);}
private:
BiNode *root;
BiNode *Creat(BiNode *bt);
void Release(BiNode *bt);
void PreOrder(BiNode *bt);
void InOrder(BiNode *bt);
void PostOrder(BiNode *bt);
};
BiNode *BiTree::Creat(BiNode *bt)
{
char ch;
cin>>ch;
if(ch=='#')
return NULL;
else
{
bt=new BiNode;
bt->data=ch;
bt->lchild=Creat(bt->lchild);
bt->rchild=Creat(bt->rchild);
}
return bt;
}
void BiTree::Release(BiNode *bt)
{
if(bt!=NULL)
{
Release(bt->lchild);
Release(bt->rchild);
delete bt;
}
}
void BiTree::PreOrder(BiNode *bt)
{
if(bt==NULL)
return;
else
{
cout<<bt->data<<" ";
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
void BiTree::InOrder(BiNode *bt)
{
if(bt==NULL) return;
else
{
InOrder(bt->lchild);
cout<<bt->data<<" ";
InOrder(bt->rchild);
}
}
void BiTree::PostOrder(BiNode *bt)
{
if(bt==NULL) return;
else
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout<<bt->data<<" ";
}
}
int main()
{
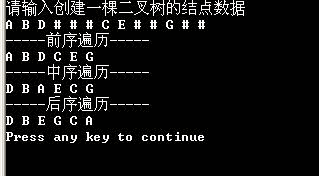
cout<<"请输入创建一棵二叉树的结点数据"<<endl;
BiTree T;
cout<<"-----前序遍历 "<<endl;
T.PreOrder();
cout<<endl;
cout<<"-----中序遍历 "<<endl;
T.InOrder();
cout<<endl;
cout<<"-----后序遍历 "<<endl;
T.PostOrder();
cout<<endl;
return 0;
}
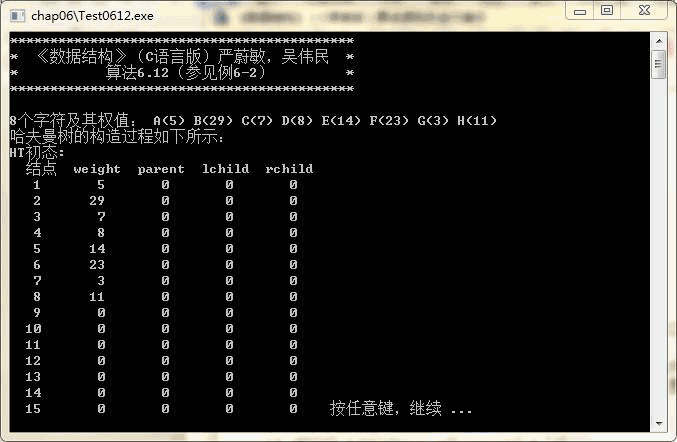
实验四:赫夫曼树
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n) {
// 算法 6.12
// w 存放 n 个字符的权值(均>0),构造哈夫曼树 HT,
// 并求出 n 个字符的哈夫曼编码 HC
int i, j, m, s1, s2, start;
char *cd;
unsigned int c, f;
if (n<=1) return;
m = 2 * n - 1;
HT = (HuffmanTree)malloc((m+1) * sizeof(HTNode)); // 0 号单元未用
for (i=1; i<=n; i++) { //初始化
HT[i].weight=w[i-1];
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for (i=n+1; i<=m; i++) { //初始化
HT[i].weight=0;
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
printf("\n 哈夫曼树的构造过程如下所示:\n");
printf("HT 初态:\n 结点 weight parent lchild rchild");
for (i=1; i<=m; i++)
printf("\n%4d%8d%8d%8d%8d",i,HT[i].weight, HT[i].parent,HT[i].lchild, HT[i].rchild);
printf(" 按任意键,继续 ...");
getch();
for (i=n+1; i<=m; i++) { // 建哈夫曼树
// 在 HT[1..i-1]中选择 parent 为 0 且 weight 最小的两个结点,
// 其序号分别为 s1 和 s2。
Select(HT, i-1, s1, s2);
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
printf("\nselect: s1=%d s2=%d\n", s1, s2);
printf(" 结点 weight parent lchild rchild");
for (j=1; j<=i; j++)
printf("\n%4d%8d%8d%8d%8d",j,HT[j].weight, HT[j].parent,HT[j].lchild, HT[j].rchild);
printf(" 按任意键,继续 ...");
getch();
}
//--- 从叶子到根逆向求每个字符的哈夫曼编码 ---
cd = (char *)malloc(n*sizeof(char)); // 分配求编码的工作空间
cd[n-1] = '\0'; // 编码结束符。
for (i=1; i<=n; ++i) { // 逐个字符求哈夫曼编码
start = n-1; // 编码结束符位置
for (c=i, f=HT[i].parent; f!=0; c=f, f=HT[f].parent)
// 从叶子到根逆向求编码
if (HT[f].lchild==c)
cd[--start] = '0';
else
cd[--start] = '1';
HC[i] = (char *)malloc((n-start)*sizeof(char)); // 为第 i 个字符编码分配空间
strcpy(HC[i], &cd[start]); // 从 cd 复制编码(串)到 HC
}
free(cd); // 释放工作空间
} // HuffmanCoding